Oppervlakte rechthoekige driehoek

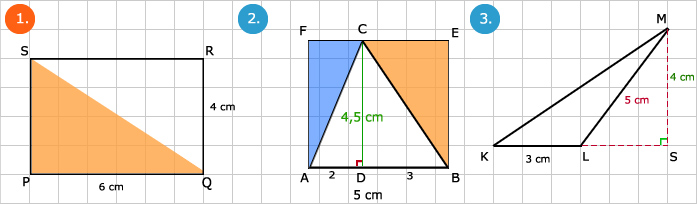
De oppervlakte van een driehoek is de helft van de oppervlakte van de rechthoek waarin je de driehoek kunt plaatsen. Bij een rechthoekige driehoek, zoals in de eerste afbeelding, is dit duidelijk te zien. Wanneer we te maken hebben met een driehoek die geen rechte hoek heeft (90°) dan is dit lastiger te zien.

Hoe bereken je de oppervlakte van een driehoek? Oppervlakte en omtrek van een rechthoekige driehoek. Rechthoekige driehoek vormt loodrecht loodlijn en schuine zijde – de langste zijde. Lengten van de zijden kan bepaald worden met de stelling van Pythagoras, en hoeken via goniometrische functies. Met de formule van Heron kan je, gegeven de lengte van elk van de drie zijden van de driehoek, de oppervlakte berekenen.

Bereken de oppervlakte van een driehoek online met de driehoek-calculator. Geef bekende waarden van de driehoek, en de. This feature is not available right now. Please try again later.

Hoewel de meest gebruikte methode om de oppervlakte van een driehoek te berekenen is het vermenigvuldigen van de halve basis met de hoogte, zijn er toch een aantal andere manieren om de. Online driehoek -rekenmachine: hoe gebruiken? Opgelet: indien meer dan velden worden ingevul worden er slechts gebruikt om de driehoek te bepalen, de andere worden (evenueel) overschreven. Men kan de oppervlakte beschouwen als opgebouwd uit n (gelijkbenige) driehoeken met basis z en een nog onbekende hoogte h. De hoogtelijn uit de tophoek naar de basis verdeelt elke driehoek in rechthoekige deeldriehoeken. Een gelijkbenige driehoek is een driehoek met twee zijden van dezelfde lengte.

Deze twee gelijke zijden hebben altijd dezelfde hoek met de basis (de derde zijde), en komen recht boven. In deze paragraaf leer je hoe je de oppervlakte van elke willekeurige driehoek kunt berekenen. De kennis uit de vorige paragraaf over hoogtelijnen speelt hier een belangrijke rol in. Driehoeken zijn onder te verdelen in drie soorten: de “gewone” driehoek met drie scherpe hoeken, de rechthoekige driehoek en de stomphoekige driehoek.

In de wiskunde gebruiken we veel formules. Met een formule kun je bijvoorbeeld de oppervlakte uitrekenen. De zijden die samen de rechte hoek vormen, worden de rechthoekszijden genoemd. Een driehoek met een rechte hoek heet een rechthoekige driehoek.

De zijde tegenover de rechte hoek heet de schuine zijde van de rechthoekige driehoek. De schuine zijde wordt ook wel hypotenusa genoemd. Hoe je dit kunt berekenen behandelen we hier. Stel je hebt driehoek ABC, zoals in de afbeelding. Je kunt de oppervlakte van deze driehoek berekenen.

De oppervlakte O van een driehoek is gelijk aan het halve product van de lengte van een zijde en de lengte van de hoogtelijn op die zijde. Anders geformuleerd: oppervlakte = basis × halve hoogte. Driehoek berekenen - Bereken eenvoudig de zijden, hoeken, oppervlakte en omtrek van een driehoek met deze online rekenmachine voor driehoeken.

Scherphoekige driehoek. Verschillende driehoekenDe rechthoekige driehoek , is zoals de naam al duidelijk maakt, een driehoek met een rechte hoek. Het berekenen: rechthoekige driehoek , zijdige driehoek , gelijkbenige driehoek en gelijkzijdige driehoek. Voer verschillende waarden, bijvoorbeeld kanten en hoek, of kanten, en klik op de knop te berekenen, voor het berekenen van andere zijden, hoeken en de oppervlakte van de driehoek.

Als de drie hoekpunten op één lijn liggen, is er geen sprake van een echte driehoek. Een van de hoeken is dan 1graden, de andere twee hoeken zijn graden. Tel de lengte van alle zijden van de driehoek bij elkaar op.

Vanuit de oudheid zijn de sinus (en cosinus) de verhoudingen in een rechthoekige driehoek. Het is hier wel van belang dat we spreken over een rechthoekige driehoek. Er zijn verschillende mogelijkheden om een hoek te berekenen. In dit voorbeeld gaan we uit van een rechthoekige driehoek en berekenen we de hoek aan de hand van sinus formule. C = hier de hoek van graden.

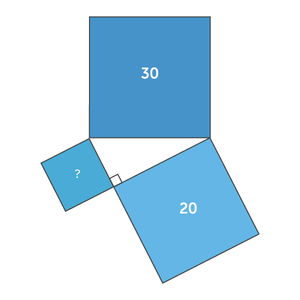
De stelling van Pythagoras 6. Allereerst wordt de stelling van Pythagoras gerelateerd aan oppervlakten: De som van de oppervlakten van de vierkanten aan de rechthoekszijden is gelijk aan de oppervlakte van het vierkant aan de schuine zijde. In woorden luidt de stelling: In een rechthoekige driehoek is de som van de kwadraten van de lengtes van de rechthoekszijden gelijk aan het kwadraat van de lengte van de schuine zijde. De sinusregel is een stelling uit de goniometrie die stelt dat in een driehoek de verhouding tussen de lengte van een zijde en de sinus van de overstaande hoek voor elk van de hoeken gelijk is aan het dubbele van de straal r van de omgeschreven cirkel. Een duidelijke definitie van de stelling van Pythagoras is, dat in een rechthoekige driehoek de som van de kwadraten van de lengtes van de rechthoekzijden, gelijk is aan het kwadraat van de lengte van de schuine zijde van de driehoek.

De rechthoekszijden van een rechthoekige driehoek hebben in wiskundige sommen een eigen naam.